Rumus atau kesamaan identitas trigonometri adalah rumus yang menyatakan hubungan antara satu fungsi trigonometri dengan fungsi trigonometri yang lainnya. Misalnya fungsi setara dengan satu ditambah fungsi atau dapat dituliskan .
Berikut ini ditampilkan beberapa kesamaan fungsi trigonometri yang penting dan sering dipakai dalam menyelesaikan masalah terkait fungsi trigonometri.
Identitas Ganjil-Genap
Berikut ini diberikan rumus untuk identitas ganjil-genap dalam trigonometri beserta dengan contoh dan pembahasannya.

Contoh 1:
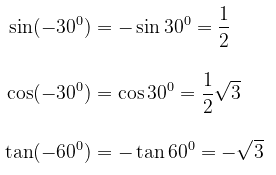
Identitas Kofungsi
Rumus identitas kofungsi merupakan salah satu identitas dalam trigonometri yang cukup penting. Identitas ini menunjukan hubungan antara fungsi trigonometri yang didasarkan pada sudut komplementer, yakni dua sudut bersebelahan yang jumlah keduanya tepat 90 derajat.

Contoh 2:

Identitas Pythagoras
Rumus identitas Pythagoras ini sering muncul dalam soal trigonometri. Sesuai namanya, rumus identitas ini diperoleh dari teorema Pythagoras. Berikut ini adalah tiga kesamaan untuk identitas pythagoras.

Contoh 3:
Buktikan bahwa persamaan identitas trigonometri berikut adalah benar.

Pembahasan:
Untuk pembuktian, kita akan menyederhanakan bentuk pada ruas kiri persamaan sehingga menjadi sama dengan ruas kanan persamaan tersebut. Perhatikan bahwa , sehingga kita peroleh

Contoh 4:
Misalkan diketahui

Nilai
Identitas Jumlah dan Selisih Dua Sudut
Berikut ini adalah rumus untuk identitas jumlah dan selisih dua sudut dalam trigonometri.

Contoh 5:
Jika diketahui . Tentukanlah nilai .
Pembahasan:
Perhatikan bahwa , sehingga dengan menggunakan identitas jumlah dua sudut untuk fungsi tangen, maka kita peroleh

Contoh 6:
Buktikan bahwa

Pembahasan:
Untuk pembuktian, kita mengambil persamaan pada ruas kiri dan disederhanakan sehingga menjadi sama dengan persamaan ruas kanan.
Contoh 7:
Sederhanakanlah bentuk persamaan berikut:
Pembahasan:
Perhatikan bahwa
Untuk bentuk dapat kita ubah menjadi
Dengan demikian, kita peroleh
Contoh 8:
Misalkan diketahui . Jika sudut adalah sudut lancip maka tentukan nilai .
Pembahasan:
Dengan menggunakan identitas sudut rangkap untuk fungsi tangen, maka kita peroleh

Identitas Setengah Sudut
Berikut ini adalah rumus untuk identitas setengah sudut beserta contoh soal dan pembahasan.

Contoh 9:
Diketahui . Tentukan nilai .
Pembahasan:
Karena , maka kita peroleh
Dengan menggunakan identitas setengah sudut untuk fungsi cosinus, maka diperoleh
Contoh 9:
Diketahui . Tentukan nilai .
Pembahasan:
Karena , maka kita peroleh
Dengan menggunakan identitas setengah sudut untuk fungsi cosinus, maka diperoleh
Contoh 9:
Diketahui . Tentukan nilai .
Pembahasan:
Karena , maka kita peroleh

Dengan menggunakan identitas setengah sudut untuk fungsi cosinus, maka diperoleh
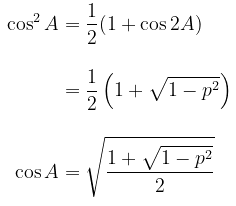
Contoh 9:
Diketahui . Tentukan nilai .
Pembahasan:
Karena , maka kita peroleh

Dengan menggunakan identitas setengah sudut untuk fungsi cosinus, maka diperoleh
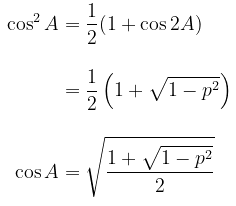




Tidak ada komentar:
Posting Komentar